Chunkable Erosion Simulation
Stop Making Ugly Terrain

A lot of game developers use procedural generation in their games. As a whole I think that's a wonderful idea, but it's clear to me that they often lack the math and physics skills to do it well. Very often I see independent game creators making procedural terrain that resembles an endless golf course. This fills my heart with sadness, and malice, and occasional alcoholism.

In an effort to cure this world of such wrong-doing, I ventured into the world of terrain generation and came up with (what I believe) to be a unique approach to the problem. The original notes I created can be found here, but they are quite messy, and not very easy to understand- which defeats the point, since game developers won't be able to read them.

Thus the birth of this explanation, which should be more coherent, and have better visuals. In this article, we will go over the difference between noise generating terrain algorithms and simulation based terrain algorithms. I will try to explain the benefits of each, and then show a technique I came up with to try and get the best of both methods.

Heightmaps And Rendering

In many games and game engines, terrain is generated and stored in "heightmaps". These are 2D arrays which store the continuous height at a discrete position (x, y) by using x and y as the indices.

If that sounds confusing, you can think of it as a top-down-view image of the terrain, where darker spots represent lower places, and lighter spots represent higher places. It would look something like this:

This is the format that we'll be working with today, there are other kinds of formats for storing terrain such as mesh-terrain, or multi-layer heightmaps. They offer better support for more complex behaviour, but are also a bit trickier to wrap your head around, so we will pretend they do not exist.

Of course it is a bit tricky to look at an image like the one above and visualize it as a piece of terrain, so I've gone through the effort of rendering them into neat gifs, like the one below:

If you're wondering why this webpage took so long to load, it's because these gifs are pretty big. With that out of the way, let's get to actually making some terrain.

Perlin Noise Isn't Special And Neither Are You

Thanks to popular cube game, Perlin noise is what everyone thinks about when they think of world generation. Perlin noise is cool enough, and it can do cool stuff- but there's nothing all that special about it. Actually, on it's own it looks awful, and I see it on it's own a lot. This fills me with thoughts of violence. Regardless, Perlin noise will be our first example of a "terrain generating noise function".

By this, I mean a function that describes a terrain in the format:

f(x, y) -> height_value

Sometimes instead they work in the format:

f(x, y, z) -> density_value

Because Perlin noise isn't really special, we'll just use a library to generate it like so.

[Code] Perlin Noise Example
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
from perlin_noise import PerlinNoise
p = PerlinNoise()
e = PerlinNoise(octaves=15)

res = 300
det = 4
ng = PerlinNoise(octaves=(2**2))
chunk = np.zeros([res, res])
for i in range(res):
    for j in range(res):
        chunk[i][j] = ng([i/res, j/res])

You'll note that the output looks like sad golf course, despite being the "magical" Perlin noise. The reason Perlin noise looks nice in Block Game and other games isn't because it's Perlin noise, but because it's added together "fractally".

Adding Stuff "Fractally"

Inspecting our golf-course, it looks bad because of a lack of details. There's major humps that might represent hills or mountains, but there are no finer details. It's too smooth and clean. You might think we would be able to fix this by adding more noise at different frequencies, and you'd be right! But if we try the naive approach...

[Code] Shitty Adding
 
1
2
3
4
5
6
7
8
9
noise_generator = []
for i in range(det):
    noise_generator.append(PerlinNoise(octaves=((i+1)**2)))

zs = np.zeros([det, res, res])
for i in range(res):
    for j in range(res):
        for k in range(det):
            zs[k][i][j] += noise_generator[k]([i/res, j/res])

The result is awful. Unless maybe we're modeling the Zhangjiajie stone pillars of Hunan.

But how come? Well, we're adding extra details by creating "higher frequency" noise (noise with more bumps-per-square-inch), but we're adding it at the same scale as the low frequency noise. In the real world, this is pretty rare. Things that cause low-frequency noise (meteors, oceans, plates shifting) are usually pretty big, and things that cause high-frequency noise (rabbits making dens, streams, rocks tumbling) tend to be pretty small. So instead, we need to scale the amplitude of the noise inversely to the frequency of the noise.

This is just a rule of thumb though, whether we scale things linearly, or by the inverse square, or even the inverse cube, it's all okay. They just represent different possible terrain configurations. Even those pillars from earlier are actually a valid terrain, just one where amplitude is scaled constantly instead.

So let's try again with the inverse square, which is often called red noise or Brownian noise.

[Code] Brownian Adding
 
1
2
3
4
z = np.zeros([res, res])
for i, hm in enumerate(zs):
    z += hm * (1.0/( (i+1)**2 ))
show_heightmap(z)

See how it looks like proper terrain now? All we had to do was acknowledge the correlation between frequency and amplitude. The simplicity of this technique is a strong motive to beat developers to death for making golf-course games.

Cell Noise

Cell noise, which is sometimes also called Voronoi noise, which is also sometimes called Worley noise, makes those creepy hole patterns that bother people with tryophobia.

This works by generating a bunch of random points, then going through every pixel in the image and settings its brightness in accordance to the \(n\) nearest points.

[Code] Voronoi Noise
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
# Naive O(n^2) solution
def gen_voronoi(size, n_points, c1=1, c2=1):
    points_x = np.random.uniform(0, size, size=n_points)
    points_y = np.random.uniform(0, size, size=n_points)
    cells = np.zeros([size, size])
    for i in range(size):
        for j in range(size):
            distances = ((points_x - i)**2 + (points_y - j)**2)
            # First closest gets multiplied by coefficient 1
            min1 = np.argmin(distances)
            cells[i][j] = min(distances)*c1
            # Then make him really big so we can find the second distance
            distances[min1] = size**2
            # and multiply it by coefficient 2fre
            cells[i][j] += min(distances)*c2

    # Rescale to be between 0 and 1
    cells -= min(cells.flatten())
    cells /= max(cells.flatten())
    return cells

If we ignore the occasional spikes, I think this looks pretty good. It's not very realistic, but the pattern and placement of the mountains feels, "mountainy".

Here, maybe this one is actually easier to see in 2D

By adjusting the c1 and c2 values we can try to simplify the output into just the "mountainy" feeling, then add it to some other noise. 

1
gen_voronoi(256, 64, c1=-1, c2=1)

We can also try our "fractal adding" trick from earlier with this. If you remember from before, when we referred to the "frequency" of the noise, we were really referring to how many bumps would occur in some section of terrain. So terrain with more bumps per square inch would be higher frequency than terrain with fewer bumps.

Using that loose definition, the "frequency" of our Voronoi digarams is how many points we add to it. Since more points would make for bumpier terrain. That means we should scale the amplitude of our Voronoi noise in accordance with how many points we add.

[Code] Fractal Voronoi
 
1
2
3
ff = np.zeros([256, 256])
for i in range(20, 30):
    ff += gen_voronoi(256, 256, i) * 1.0/i

Again, here we can illustrate that Perlin noise really isn't that special, there are tons of different noise algorithms that can give you nice terrain provided you add the layers of noise together with the right technique.

Pink Noise

Pink noise is a method of layering noise not dissimilar from the "fractal adding" technique we saw earlier. We're essentially just going to do what we did above, but using a base of white noise.

Specifically with Pink Noise, the "power spectral density" must be of the form \[ S(f) \propto {\frac {1}{f^{\alpha }}} \] Where for our sake \(\alpha=0.5\), and \(f\) is the frequency of any given signal in the noise.

If the term "power spectral density" intimidates you, you may think of it as an amplitude at any given frequency. In actuality (for this specific scenario) the amplitude is the square root of the power.

The primary reason why Pink Noise is important is because power spectral density sounds like cool wizard shit and I am a cool wizard .

Oh and it captures the "fractal adding" idea from before or whatever, relating it to real life electromagnetic noise and connecting the dots to the sacred geometry that exists all around us- but often escapes the view of our naive mortal minds.

Mostly it's the cool wizard thing though.

We can generate pink noise easily by entering "Fourrier space", which is a fancy way of saying "the vectorspace of all the decomposed frequencies in a signal". So all we have to do is compute the frequencies that make up a signal with the Fast Fourrier Transform, then scale down the ones that move away from the center frequency. Because the equation above only requires it be proportional, it doesn't actually matter where we centre this from a math standpoint, from a "our numpy array is only so big" standpoint it totally matters.

Anyway then we do the opposite of a Fourrier transform, which is just adding up a bunch of sine waves, and that's Pink Noise.

[Code] Generating Pink Noise
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def gen_pink(size=128, scale=0.25):
  # Generate white noise
  white = np.random.normal(size=(size, size))

  # Fourrier transform shift to centre lower frequency
  white_ft = np.fft.fftshift(np.fft.fft2(white))

  # Create a field such that as we go further from the origin
  # frequency goes up
  hsize = size / 2 # since we're centering [0, size] -> [-size/2, +size/2]
    
  # np.hypot finds the euclidean distance to the center (hypoteneuse)
  # np.ogrid just makes two vectors [-size/2, size], one vertical one
  # horizontal, the final result is a 2d matrix of distance to the middle
  # x[i][j] = distance (i,j) -> (0, 0)
  freq = np.hypot(*np.ogrid[-hsize:hsize, -hsize:hsize])

  # Now we scale the noise in fourier space so that its frequency matches
  # the definition of pink noise (its squared so brownian noise maybe?)
  pink_ft = np.divide(white_ft, freq**2,
    out=np.zeros_like(white_ft), where=freq!=0)

  # Leave fourrier space
  pink = np.fft.ifft2(np.fft.ifftshift(pink_ft)).real

  # Scale the noise to be between 0 and 1
  lo, hi = np.min(pink), np.max(pink)
  pink = (pink - lo) / (hi - lo)
  return pink
Benefits of Using A Noise Function

Okay so we know what noise functions are now, but why would we use them?

Speed:

Most noise algorithms are pretty quick to generate, which allows us to generate the world in real-time, as the player moves through it. That also allows us to have a world of infinite size with no loading screens.


Chunking:

Chunking! The noise function describes a terrain of infinite size, but we can load individual parts of that terrain (known as chunks) as we need them, without having to load any other chunks around them. For example, if the player teleports from (0, 0) to (100, 0) we only need to generate those two chunks, not all the chunks between them, such as (20, 0) or (40, 0).


Saving:

If we're going to modify this terrain, we only need to store the changes, not the whole chunk. Because we can just re-generate the chunk, then re-apply the changes. You can imagine that if our chunk size was 16x16x256, saving the whole 65,636 spaces might be pretty cumbersome.

Simulation Based Terrain Generation

Noise algorithms are cool, but they have limitations. Since it has to be possible to generate each position on it's own, it isn't possible for the information at one position to depend on the information of another position.

Simulation based terrain generation is different. We accept a finite terrain, and a lengthy generation process, then we run a simulation to re-create the phenomenon real terrain experience.

An example of a simulation based terrain generator is hydraulic erosion, which we're about to go over.

Hydraulic Erosion

Terrain is usually made of like dirt and shit. When water moves over dirt and shit, it picks some of it up. But then when the water evaporates, the dirt (and other shit) does not evaporate. This process shapes mountains, rivers, and valleys, giving them cool features.

Chemical engineers are known for playing with dirt and picking their noses. In fact, they came up with an easy way to measure the transfer of dirt and shit using some handy differential equations, but because chemical engineers are all squares, they say "sediment" not "dirt and shit". \[ \frac{dc}{dt} = k(c_{eq} - C) \] Where \(k\) is the mass transfer coefficient, \(c_{eq}\) is the equilibrium concentration, and \(C\) is the concentration (of sediment in the flowing water).

Translated from an equation, this essentially says:

  • you can only put so much dirt in water
  • if the water is saturated with dirt it won't pick up more dirt
  • if the water doesn't have enough dirt, it will pickup more dirt.

Using this explanation, we will model the path of a single drop of water flowing over our heightmap. The drop itself is easily governed by 2D Newtonian mechanics, where the "acceleration" will be the gradient of the heightmap at whatever position the drop is at. Of course, this isn't a completely accurate model, but erosion isn't done by a single drop of water- it's done by thousands, so our simulation has to be pretty quick.

[Code] Drop Class
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# I will be simulating this from the perspective of a single drop, but this is PAINFULLY SLOW
# it is much better to keep the attributes of the drop spread out in numpy array. I chose this
# method instead because I thought it would be easier to visualize. If you're just here to
# copy paste code, scroll to the bottom and take the better simulation!

class Drop:
    def __init__(self, x, y):
        self.pos = np.array([x, y], dtype='float64')
        self.vel = np.array([0.0, 0.0])
        self.sediment = 0.0
        self.volume = 1.0
        self.prev_height = None

    def move(self, dt, accel):
        self.speed += dt*accel/(self.volume*0.1) # 0.1 being density
        self.pos += dt*self.vel
        self.vel *= 0.99 # inverse friction

    def erode(self, dt, height_at_pos, deposition_rate, evaporation_rate):
        # Don't erode on the first tick, since we can't compute the derivative
        if self.prev_height is None:
            self.prev_height = height_at_pos
            return 0.0

        # Then based off that derivative we can compute mass transfer
        c_eq = self.volume * np.hypot(*self.speed)*(height_at-pos - self.prev_height)
        if c_eq < 0.0: c_eq = 0.0

        # The further we are from the equilibrium, the faster we deposit
        # dirt.
        cdiff = c_eq - self.sediment 
        self.sediment += dt*cdiff*deposition_rate

        # Evaporate a bit of water
        self.volume *= self.volume * (1.0 - 0.000*dt)

        # Return the difference in height that should have been made at this position
        return dt*self.volume*deposition_rate*cdiff

That gives us a little drop that rolls down the hills of our world, evaporating and eroding as he passes. But as mentioned before, erosion is done by many drops of water, so we'll have to write a function to apply many of them to a heightmap.

[Code] Simulation
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def erode_heightmap(heightmap, cycles=100):
    # Get our settings in order
    width, length = heightmap.shape
    dt = 1.0
    evaporation_rate = 0.00001
    deposition_rate = (4.0/6.0)

    # Then make a random drop somewhere random
    drop = Drop( random.randint(0, width-1), random.randint(0, length-1))

    for cycle in range(cycles):
        # Find his position in discrete coordinates
        posx, posy = drop.pos
        posx, posy = int(posx-1), int(posy-1)

        # Then do erosion there
        heightmap[posx, posy] -= drop.erode(
            dt,
            heightmap[posx, posy],
            evaporation_rate,
            deposition_rate
        )

        # Then we'll do that whole "physics" thing or whatever
        accl = np.array(single_gradient(heightmap, posx, posy))
        drop.move(dt, accl)

        # Then if the drop runs out of water or goes out of bounds, make a new one
        if (drop.pos[0] > width or drop.pos[1] > length or
            drop.pos[0] < 0 or drop.pos[1] < 0 or drop.volume < 0.01):
            drop = Drop(random.randint(0, width-1), random.randint(0, length-1))

Then all we have to do is call our erosion function. Below we'll use a noise generating algorithm called "pink noise", which I'll explain in the next section, but for now just think of it like Perlin noise.

In order to make the effects of the erosion simulation more visible, let's erode this terrain a lot. This should give us smooth peaks, and a deep lake.

[Code] Running it
 
1
2
3
4
5
6
7
8
gr = gen_pink(size=128)
og = np.copy(gr)
i=3
cycles = 1000000*6
erode_heightmap(
    gr, dt=0.25, cycles=cycles,
    evaporation_rate=0.00001, friction=0.0001, deposition_rate= (1.0/6.0)*(i+1)
)

Then we can try again with a lighter pass that might better preserve some of the original features.

[Code] A Lighter Pass
 
1
2
3
4
5
6
7
8
gr = gen_pink(size=128)
og = np.copy(gr)
i=3
cycles = 1000000*3
erode_heightmap(
    gr, dt=0.25, cycles=cycles,
    evaporation_rate=0.00001, friction=0.0001, deposition_rate= (1.0/6.0)*(i+1)
)

If we ran this algorithm for too long, we'd get a completely smoothed out plane, but running the algorithm too long isn't the problem. Simulated algorithms take a really long time to run, because they have to time-step over each and every chunk.

In fact the terrain we generated is only 128 by 128 units, but this alone takes about 10 minutes to generate on this computer. Now, it is a crummy Python script, written without much consideration for performance, but there's a bigger problem with scaling up the terrain size.

We'll get back to that scaling issue, but first let's go over the next kind of erosion.

Thermal Erosion

Due to esoteric magic, materials get bigger or smaller when you heat them up. Actually, it's only really water that gets bigger when it cools down- but it still gets bigger if you heat it up too much. Like I said, it's all due to a process called esoteric magic.

It's unfortunate but many things in the universe are caused by esoteric magic, so to distinguish them, scientists have come up with the convention of naming esoteric phenomenon after Minecraft mods. This expanding/contracting with temperature is called Thermal Expansion.

Anyway, when the seasons change the temperature we get "Thermal Expansion" which causes loose bits of sediment to break free. They form little piles, which for some reason have a particular angle they like to fall over at. Essentially, if you make a pile of dirt, it can reach a certain angle before it falls over and repositions itself. We call that the Angle of Repose, and it is named after this Minecraft mod .

Anyway we can write a silly little function to go through our heightmap, and check when the angle is too steep somewhere (via the gradient), then apply a gaussian blur to the spots that should have fallen over. This has the added benefit of smoothing out our somewhat crunchy simulation.

[Code] Thermal Erosion Through Blurring
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
# I stole this gaussian blur code off the internet. This is okay 
# because intelectual property is a conspiracy made up by The Government.

def gaussian_blur(a, sigma=1.0):
    freqs = tuple(np.fft.fftfreq(n, d=1.0 / n) for n in a.shape)
    freq_radial = np.hypot(*np.meshgrid(*freqs))
    sigma2 = sigma**2
    g = lambda x: ((2 * np.pi * sigma2) ** -0.5) * np.exp(-0.5 * (x / sigma)**2)
    kernel = g(freq_radial)
    kernel /= kernel.sum()
    return np.fft.ifft2(np.fft.fft2(a) * np.fft.fft2(kernel)).real

def thermal_erosion(heightmap, heightmap_grad, repose_threshold, cell_width):
    delta = grad / cell_width
    smoothed = gaussian_blur(terrain, sigma=1.5)
    result = np.select([np.abs(delta) > repose_slope], [smoothed], terrain)
    return result

Occaisionally running this while we do our hydraulic erosion simulation will give us much nicer results, because it prevents the creation of unnaturally steep layers.

I think these results very evidently give a nicer, more realistic, look.

Scaling The Terrain

I told you we'd get back to this.

You might think that a square terrain with an edge length of 256 is twice as big as one with an edge length of 128. That's because you're stupid and dumb. A terrain with an edge of 128 has an area of 128^2 or 16,384 and a terrain with an edge length of 256 has an area of 256^2 or 65,536.

The degree of the erosion on our terrain can be measured in "raindrops per unit squared" or "how much water hits the ground divided by how much ground there is". That means to erode a terrain of edge length 256 the same amount we eroded the terrain of edge length 128, we need to pour about 4 times as much water.

Simulating that many drops will take a while, and at the end of it we'll be left with only a 256x256, not a lot of detail. If we wanted to make a terrain of 10,000 by 10,000 we'd be screwed.

It might be possible to improve this performance using GPU parallelization, but that's really a bandage for a bigger problem- which is that our algorithm is \(O(n^2)\) where \(n\) is the edge length of the terrain.

We can start to remedy this by improving the performance of our simulation through simple optimization techniques. Python is slow, and object orientation is slow, and so it is much more efficient to use Numpy to perform all the simulation steps.

The code below is taken from this Github and only slightly modified to fit this articles format, and make it self contained so you can steal it and put it in your game- and stop making sad golf courses.

[Code] Numpy Simulation
 
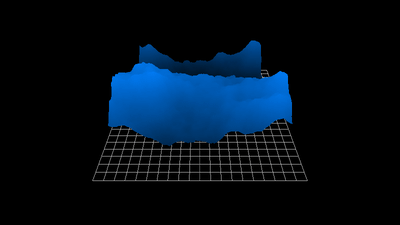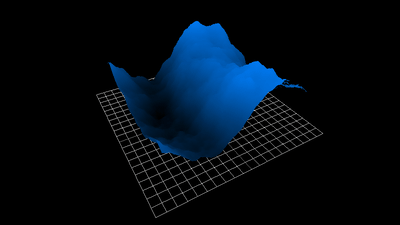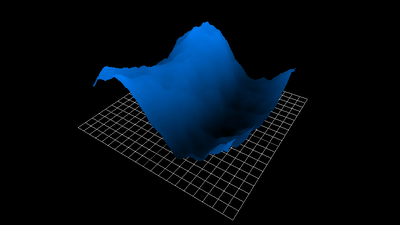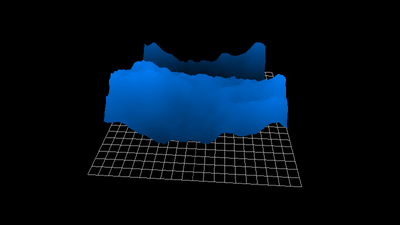
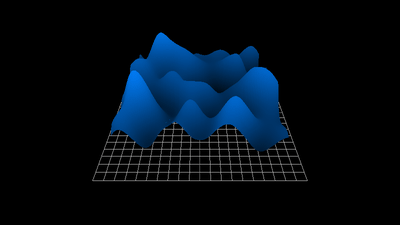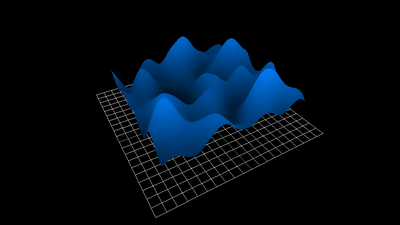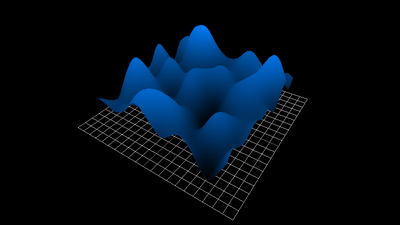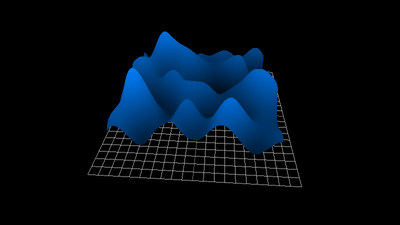
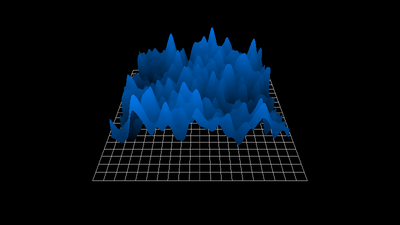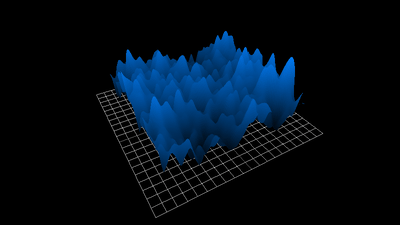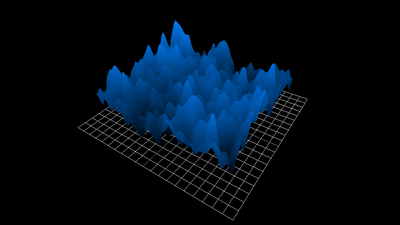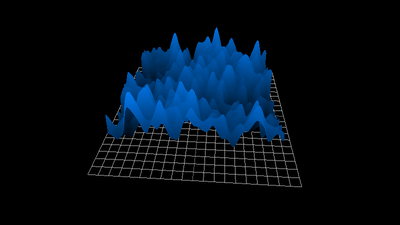
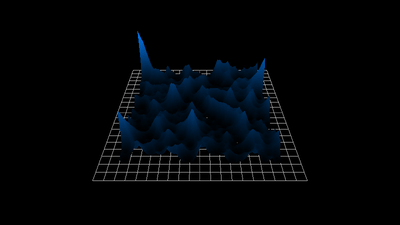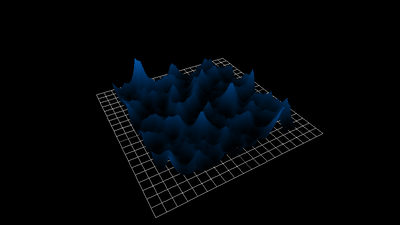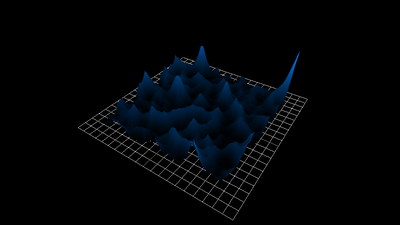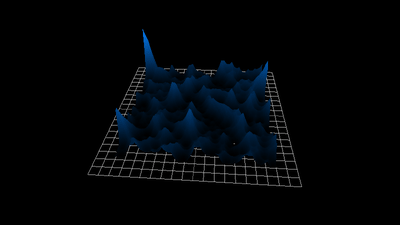
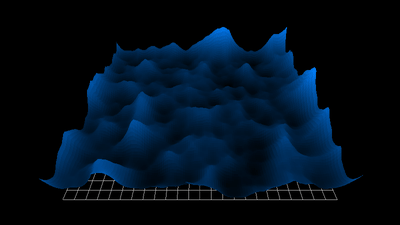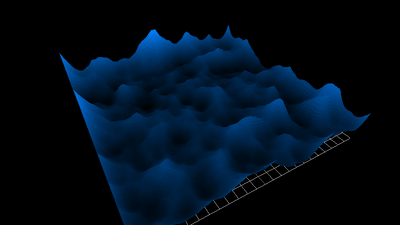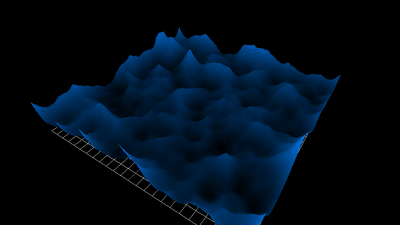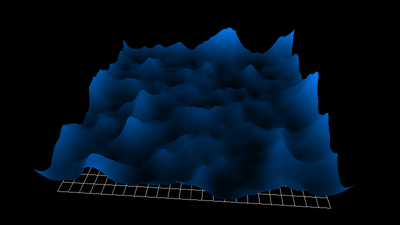
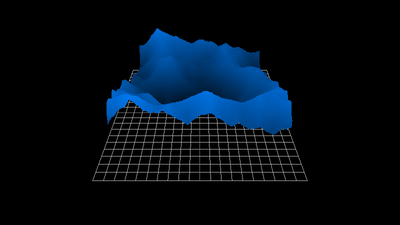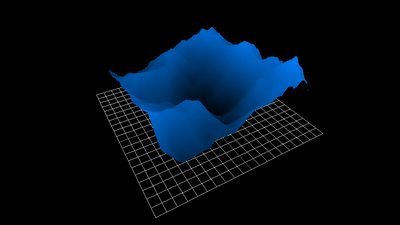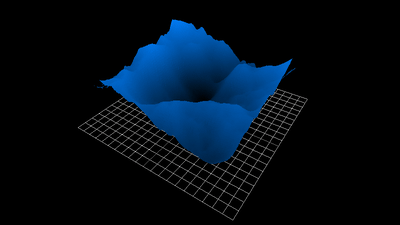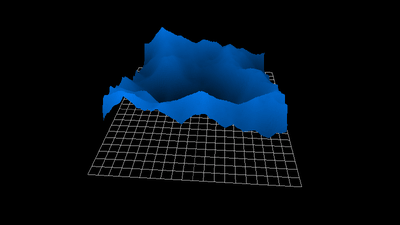
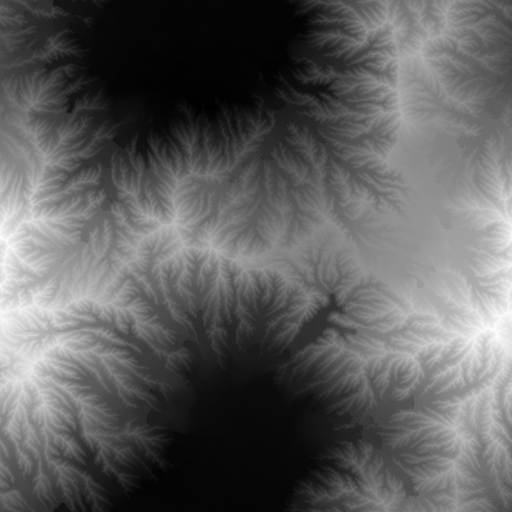
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
import numpy as np

def lerp(x, y, a): return (1.0 - a) * x + a * y

def simple_gradient(a):
  dx = 0.5 * (np.roll(a, 1, axis=0) - np.roll(a, -1, axis=0))
  dy = 0.5 * (np.roll(a, 1, axis=1) - np.roll(a, -1, axis=1))
  return 1j * dx + dy

def displace(a, delta):
  fns = {
      -1: lambda x: -x,
      0: lambda x: 1 - np.abs(x),
      1: lambda x: x,
  }
  result = np.zeros_like(a)
  for dx in range(-1, 2):
    wx = np.maximum(fns[dx](delta.real), 0.0)
    for dy in range(-1, 2):
      wy = np.maximum(fns[dy](delta.imag), 0.0)
      result += np.roll(np.roll(wx * wy * a, dy, axis=0), dx, axis=1)

  return result

def gaussian_blur(a, sigma=1.0):
  freqs = tuple(np.fft.fftfreq(n, d=1.0 / n) for n in a.shape)
  freq_radial = np.hypot(*np.meshgrid(*freqs))
  sigma2 = sigma**2
  g = lambda x: ((2 * np.pi * sigma2) ** -0.5) * np.exp(-0.5 * (x / sigma)**2)
  kernel = g(freq_radial)
  kernel /= kernel.sum()
  return np.fft.ifft2(np.fft.fft2(a) * np.fft.fft2(kernel)).real

def normalize(x, bounds=(0, 1)):
  return np.interp(x, (x.min(), x.max()), bounds)

def fbm(shape, p, lower=-np.inf, upper=np.inf):
  freqs = tuple(np.fft.fftfreq(n, d=1.0 / n) for n in shape)
  freq_radial = np.hypot(*np.meshgrid(*freqs))
  envelope = (np.power(freq_radial, p, where=freq_radial!=0) *
              (freq_radial > lower) * (freq_radial < upper))
  envelope[0][0] = 0.0
  phase_noise = np.exp(2j * np.pi * np.random.rand(*shape))
  return normalize(np.real(np.fft.ifft2(np.fft.fft2(phase_noise) * envelope)))

def sample(a, offset):
  shape = np.array(a.shape)
  delta = np.array((offset.real, offset.imag))
  coords = np.array(np.meshgrid(*map(range, shape))) - delta

  lower_coords = np.floor(coords).astype(int)
  upper_coords = lower_coords + 1
  coord_offsets = coords - lower_coords 
  lower_coords %= shape[:, np.newaxis, np.newaxis]
  upper_coords %= shape[:, np.newaxis, np.newaxis]

  result = lerp(lerp(a[lower_coords[1], lower_coords[0]],
                     a[lower_coords[1], upper_coords[0]],
                     coord_offsets[0]),
                lerp(a[upper_coords[1], lower_coords[0]],
                     a[upper_coords[1], upper_coords[0]],
                     coord_offsets[0]),
                coord_offsets[1])
  return result

def apply_slippage(terrain, repose_slope, cell_width):
  delta = simple_gradient(terrain) / cell_width
  smoothed = gaussian_blur(terrain, sigma=1.5)
  should_smooth = np.abs(delta) > repose_slope
  result = np.select([np.abs(delta) > repose_slope], [smoothed], terrain)
  return result

def erode(heightmap: np.array, cycles=1.0):
    full_width = heightmap.shape[0]
    dim = heightmap.shape[0]
    shape = heightmap.shape
    cell_width = full_width / dim
    cell_area = cell_width ** 2

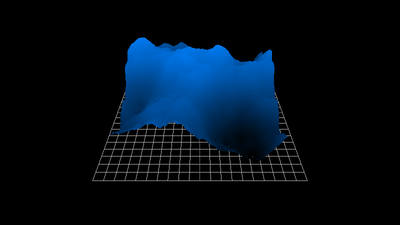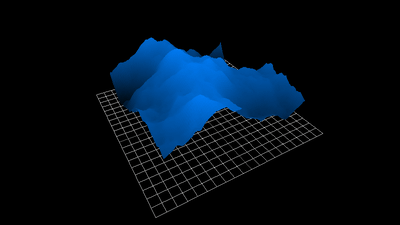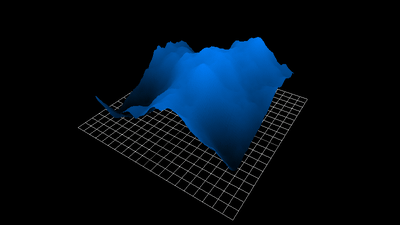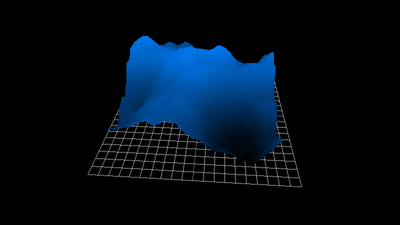
    # Generate terrain from noise
    #heightmap = fbm(shape, -2.0)
    
    water = np.zeros_like(heightmap)
    velocity = np.zeros_like(heightmap)
    sediment = np.zeros_like(heightmap)
    
    # Water constants
    rain_rate = 0.0008 * cell_area
    evaporation_rate = 0.0005

    # Slope constants
    min_height_delta = 0.05
    repose_slope = 0.03
    gravity = 30.0
    gradient_sigma = 0.5
    
    # Sediment constants
    sediment_capacity_constant = 50.0
    dissolving_rate = 0.25
    deposition_rate = 0.001
    
    for _ in range(int(1.4*dim*cycles)):
        water += np.random.rand(*shape) * rain_rate
        # Compute normalized gradient
        gradient = np.zeros_like(heightmap, dtype='complex')
        gradient = simple_gradient(heightmap)
        gradient = np.select(
            [np.abs(gradient) < 1e-10],
            [np.exp(2j * np.pi * np.random.rand(*shape))],
            gradient
        )
        gradient /= np.abs(gradient)

        # Compute the difference between the current height and the
        # height offset by the gradient
        neighbor_height = sample(heightmap, -gradient)
        height_delta = heightmap - neighbor_height
            
        # See the notes about this equation in a previous section.
        sediment_capacity = ((np.maximum(height_delta, min_height_delta) / cell_width) * velocity * water * sediment_capacity_constant)
        
        deposited_sediment = np.select(
            [
              height_delta < 0, 
              sediment > sediment_capacity,
            ], [
              np.minimum(height_delta, sediment),
              deposition_rate * (sediment - sediment_capacity),
            ],
            dissolving_rate * (sediment - sediment_capacity)
        )

        deposited_sediment = np.maximum(-height_delta, deposited_sediment)

        sediment -= deposited_sediment
        heightmap += deposited_sediment
        sediment = displace(sediment, gradient)
        water = displace(water, gradient)

        # Smooth out steep slopes
        heightmap = apply_slippage(heightmap, repose_slope, cell_width)

        # Update velocity
        velocity = gravity * height_delta / cell_width

        # Apply evaporation
        water *= 1 - evaporation_rate
    
    return heightmap

#pyplot.imsave("/static/erosion_imgs/efficient1.png", erode(fbm([512, 512], -2)), cmap='grey')

Yeah it looks snazzy when it's higher resolution, doesn't it? But this still took 3 minutes to generate on The Computer, and it's only 512x512... So we're going to have to get a bit clever if we want to do this in real time in a computer game.

Getting A Headstart

All the images above start with Brownian noise, then pass a chunk of it to the simulation to erode. Brownian noise is a good start for terrain, but it ignores important aspects such as the angle of repose, and total mass displacement. That's a complicated way of saying it puts dirt in places where the simulation is just going to have to move it. We probably spend a lot of our simulation time just moving big chunks of dirt from the tops of hills to the bottom of hills.

Let's try and write a noise algorithm that already looks a little bit eroded, in terms of bulk placement. We'll be taking some inspiration from this paper, and from another idea called "The Gradient Trick" which comes from this mage.

We'll start with Pink Noise instead of Brownian noise, because that's what the nerds at MIT did. I don't know if it really matters to be honest, but when performing sacred magic rites you should always follow the instructions exactly. We'll add Voronoi noise to it. This makes it look worse- but it strongly suggests where the mountain ridges should go. This is important for the chunkability of the algorithm.

Using our erosion-like noise, we only really need to run the erosion system for \(\frac{1}{4}^{th}\) or \( \frac{1}{5}^{th} \) as many cycles. In fact, I find it easy to make the terrain "over-eroded" where it looks too smooth and artificial.

[Code] Headstart With Noise
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
def headstart_noise(size=256):
    p_pink = 0.85
    p1 = 2.5*gen_voronoi(size, n_points=50)*(1 - p_pink) + gen_pink(size)*p_pink
    return p1


p1 = headstart_noise(size=512)
d1 = erode(p1, cycles=0.5)

print("<center>")
show_img(p1, width=30)
print(" ", end='')
show_img(d1, width=30)
print("</center>")

Generating the terrain like this takes much less time, but it also means the majority of the terrain data is predictable. That means we can try to write a chunking algorithm for it!

Writing a Chunking Algorithm

The simplest approach here is obvious. Just generate pink noise for x,y and x+256,y+256, and erode both chunks. This actually almost works, but we can see a seam at the edge of each chunk.

[Code] Naive Chunking
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
total = np.copy(gen_pink(512))
chunk_a = total[0:256, 0:256]
chunk_b = total[0:256, 256:512]

print("<center>")
show_img(np.concat([chunk_a, chunk_b], axis=1), width=45)
print(" ", end='')
ea = erode(chunk_a, cycles=0.2)
eb = erode(chunk_b, cycles=0.2)
show_img(np.concat([ea, eb], axis=1), width=45)
print("</center>")

The easiest way to fix that is by slowly transitioning from one chunk to the other. We can does this through linear interpolating. This is fast and looks mostly okay- but it doesn't make hydraulic sense anymore. Water in one chunk doesn't change the flow in water from another chunk. It only looks okay because all the large features come from the noise algorithm (and so are coherent across chunks).

So while it's very unlikely we'd see a sudden shear cliff as we transition chunks, rivers might dry out quickly, and lakes will appear in places where they should have drained.

[Code] Stitching Through Lerp
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def stitch_chunk_right(chunka, chunkb, seam_size=8):
    seam = np.zeros( [chunka.shape[0],  seam_size] )
    seamx_start = chunka.shape[0] - seam_size
    for i in range(seam_size):
        for j in range(chunka.shape[1]):
            seam[j, i] = chunka[j, seamx_start+i]*(1.0 - i/seam_size) + chunkb[j, i] * (i/seam_size)
    return chunka[0:chunka.shape[1], 0:seamx_start], seam, chunkb[0:chunkb.shape[1], seam_size:]

sa, se, sb = stitch_chunk_right(ea, eb, seam_size=40)
print("<center>")
show_img(np.concat([sa, se, sb], axis=1), width=70)
print("</center>")

Personally I feel this is acceptable for most use cases. It's A LOT nicer looking than the golf courses I see produced. However, as a Mage, I would like to make this as seamless as possible. Even if (using the current system) it is impossible to make it fully coherent.

We can improve the coherency of the chunks by running the erosion simulation on the border. Of course, this then creates a less pronounced seam near the borders of the second simulation, so we have to go back and forth chasing this little seam- and each time we do it gets a little smaller.

You ever do that with like a dustpan? Like you try and dust up all the dirt but it leaves that little line, so you sweep perpendicularly to it but then it leaves like another little line? It's like that pretty much.


It took me a long time to find an image of this.
[Code] Dust Pan Thing
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#total = np.copy(headstart_noise(512))
total = np.copy(fbm([1024, 1024], -2))
chunk_size=128
half_chunk = chunk_size//2
cycles = 0.5

chunk_a = total[0:chunk_size, 0:chunk_size]
seed = total[0:chunk_size, half_chunk:half_chunk+chunk_size]
chunk_b = total[0:chunk_size, chunk_size:chunk_size*2]

chunk_area = total[0:chunk_size, 0:chunk_size*2]
#chunk_c = total[0:chunk_size, chunk_size*2:chunk_size*3]

# We will update it in this funny way to preserve the reference
seed += -seed + erode(seed, cycles=cycles)
chunk_a += -chunk_a + erode(np.copy(chunk_a), cycles=cycles)
chunk_b += -chunk_b + erode(np.copy(chunk_b), cycles=cycles)

# Some solution with 0 padding before eroding?


print("<center>")
show_img(np.concat([chunk_a, seed, chunk_b], axis=1), width=60)
show_img(chunk_area, width=60)
print("</center>")

There's probably a more intelligent way to fix this, but I'm just going to lerp the lines...

[Code] Common Eroded Seam & Lerp
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
total = np.copy(gen_pink(512))
overlap = 40
chunk_a = total[0:256+overlap, 0:256+overlap]
chunk_b = total[0:256+overlap, 256-overlap:512]

def stitch_chunk_right(chunka, chunkb, seam_size=8):
    seam = np.zeros( [chunka.shape[1],  seam_size] )
    seamx_start = chunka.shape[1] - seam_size
    for i in range(seam_size):
        for j in range(chunka.shape[1]):
            seam[j, i] = chunka[j, seamx_start+i]*(1.0 - i/seam_size) + chunkb[j, i] * (i/seam_size)
    return chunka[0:chunka.shape[1], 0:seamx_start], seam, chunkb[0:chunkb.shape[1], seam_size:]


print("<center>")
show_img(np.concat([chunk_a, chunk_b], axis=1), width=45)
print(" ", end='')
ea = erode(chunk_a, cycles=0.2)
eb = erode(chunk_b, cycles=0.2)
show_img(np.concat([ea, eb], axis=1), width=45)

eac = ea[:, :256+overlap//2]
ebc = eb[:, overlap//2:]

aa, ss, bb = stitch_chunk_right(eac, ebc, seam_size=overlap)
show_img(np.concat([aa, ss, bb], axis=1), width=45)
print("</center>")
Conclusions

The conclusion is if I catch your ass using pure perlin noise again, for anything other than a golf simulator you make me sad and you should feel bad about yourself.

I actually have a fair amount more on this topic to share, but this is kind of long for one notebook page. I have also done some experiments on monitoring where the water flows on these terrains, using it to create a "water map", and using that to indicate not only where streams and lakes should be, but where certain types of vegetation should grow.